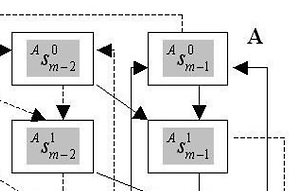
Złożoność półgrupy charakterystycznej sumy prostej automatów
asynchronicznych silnie spójnych i ustalonych analogów ich rozszerzeń dla każdego słowa z języka
Suma+ = (sigma_0 & sigma_1)+
1
Instytut Pojazdów Szynowych „TABOR”
Data publikacji: 02-11-2010
Rail Vehicles/Pojazdy Szynowe 2010,4,34-49
STRESZCZENIE
Półgrupa charakterystyczna automatu ingeruje w algorytm obliczeniowy uogólnionych homomorfizmów
automatów, zatem wyznaczenie złożoności półgrupy charakterystycznej pozwala na oszacowanie
złożoności obliczeniowej uogólnionych homomorfizmów dla innych klas automatów. W
zakresie modelu matematycznego koncepcja ustalonego analogu rozszerzenia automatu A
związanego z izomorfizmami g0, g1,..., gq-1, gdzie q stopień rozszerzenia, przy odpowiednich
założeniach symuluje automat zmienny w czasie. Automat zmienny w czasie jest adekwatnym modelem
matematycznym dla wielu procesów technicznych i obliczeniowych czasu rzeczywistego. Automaty te
symulują pracę kilku automatów za pomocą jednego automatu zmiennego w czasie. Sumę prostą
automatów można uważać za realizację
– odpowiednio sekwencyjnych obliczeń.
REFERENCJE (29)
1.
Arbib M.A.: Algebraic theory of machines languages and semigroups, Acadimic Press, New York and London 1968.
2.
Aho A.V., Hopcrofy I.E., Ullman I.D.:Projektowanie i analiza algorytmów komputerowych,PWN,Warszawa 1983.
3.
Barnes B.: On the groups of automorhism of strongly connected automata, Math.Syst. Theory 4, 4 (1970).
4.
Beatty I. C.;On some properties of semigroup of a machine which are preserved under state minimization, Information and Control 11, 3 (1970).
5.
Beyga L.: On periodic sums of automata associated with isomorphism, Foundations of Control Enginiering 1,3 (1976).
6.
Bocian S.: Złożoność półgrupy charakterystycznej automatów asynchronicznych i ich rozszerzeń, Prace Instytutu Podstaw Informatyki Polskiej Akademii Nauk nr 552, Warszawa, 1984.
7.
Bocian S., Mikołajczak.: Computational aspect of assigning characteristic semigroup asychronous automata and their extensions, Colloqia Mathematica Societatis Janos Bolyai nr 44,Amsterdam, New York, Budapest, 1985.
9.
Bocian S.: The complexity of semigroup characterization of asynchronous strongly connection automation and thier extensions, Computational topology and geometry and computation in teaching mathematic, Universal de Sevilla,1987.
10.
Bocian S.: A new method of calculating the smallest common multiple, Computational topology and geometry and computation in teaching mathematic, Universal de Sevilla,1987.
11.
Bocian S.: Nowy sposób wyznaczania najmniejszej wspólnej wielokrotności liczb naturalnych, jako model matematyczny automatu w technice komputerowej, Pojazdy szynowe 1/2002.
12.
Bocian S.: Złożoność pólgrupy charakterystycznej automatów asynchronicznych silnie spójnych ustalonych analogów ich rozszerzeń związanych z izomorfizmami, TRANSCOMP - XIII INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCES, INDUSTRY AND TRANSPORT, Zakopane 2009.
13.
Bocian S.: Nowy sposób wyznaczania najmniejszej wspólnej wielokrotności liczb naturalnych, OR – 9834 (praca nie pu- blikowana).
14.
Bocian S: Złożoność półgrupy charakterystycznej sumy pro- stej i iloczynu prostego automatów asynchronicznych silnie spójnych, TRANSCOMP - XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCES, INDUSTRY AND TRANSPORT, Zakopane 2010.
15.
Bocian S: Złożoność półgrupy charakterystycznej sumy pro- stej automatów asynchronicznych silnie spójnych ustalonych analogów rozszerzeń związanych z izomorfizmami, TRANSCOMP - XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCES, INDUSTRY AND TRANSPORT, Zakopane 2010.
16.
Bocian S: Złożoność półgrupy charakterystycznej iloczynu prostego automatów asynchronicznych silnie spójnych usta- lonych analogów rozszerzeń związanych z izomorfizmami, TRANSCOMP - XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCES, INDUSTRY AND TRANSPORT, Zakopane 2010.
19.
Grzymała-Busse J.W.: On the periodic reprezentation and reducibility of periodic automata, J.Assoc. Comput. Mach. 16, 3(1969).
20.
Grzymała-Busse J.W.: On the endomorphisms of finite automata, Mach. Syst. Theory 4, 4 (1970).
21.
[21}Grzymała-Busse J.W.: Podautomaty automatów skończonych związane ze zmianączsu pracy, Politechnika Poznańska, Rozprawy nr.46, Poznań, 1972.
22.
Kerntopf P.: Podstawowe pojęcia matematyczne w teorii automatów, PWN, Warszawa 1967.
23.
Mikołajczak B., Miądowicz Z.: On the automorphisms group of strongly related automata and structural properties of finite automata and extensions, Foundations of Control Engineering,1,2 (1976).
24.
Mikołajczak B.: On the structure of cyclic automata and their generalized periodic sums, Technical Report, Computer Sci- ence Department, Cornell University, 1977.
25.
Mikołajczak B.: On the structure of cyclic automata and their generalized periodic sums, Foundations of Control Engi- neering, 3,1 (1978).
26.
Mikołajczak B.: Uogólnione przekształcenia okresowe auto- matów skończonych, Politechnika Poznańska, Rozprawy nr.98, Poznań 1979.
27.
Mikołajczak B.: Algebraiczna i strukturalna teoria automa- tów, PWN Warszawa - Łódź, 1985.
28.
Mikołajczak B.: Przekształcenia i złożoność obliczeniowa problemów w teorii automatów, PWN Warszawa – Poznań, 1988.
29.
Oehmke R.H.: The semigroup of a strongly connected automation, Math. Systems Theory, 15 (178).
Udostępnij
Przetwarzamy dane osobowe zbierane podczas odwiedzania serwisu. Realizacja funkcji pozyskiwania informacji o użytkownikach i ich zachowaniu odbywa się poprzez dobrowolnie wprowadzone w formularzach informacje oraz zapisywanie w urządzeniach końcowych plików cookies (tzw. ciasteczka). Dane, w tym pliki cookies, wykorzystywane są w celu realizacji usług, zapewnienia wygodnego korzystania ze strony oraz w celu monitorowania ruchu zgodnie z Polityką prywatności. Dane są także zbierane i przetwarzane przez narzędzie Google Analytics (więcej).
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.