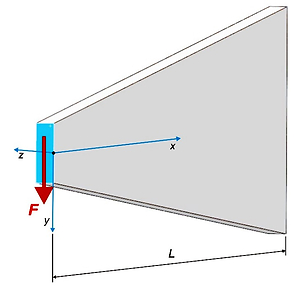
Stress state in the tapered beam bending –
Analytical and numerical FEM studies
1
Sieć Badawcza Łukasiewicz -
Instytut Pojazdów Szynowych „TABOR”
Publication date: 2019-05-03
Rail Vehicles/Pojazdy Szynowe 2019,2,1-8
KEYWORDS
ABSTRACT
The paper is devoted to comparative analysis of the stress state in bending of a tapered
cantilever beam, calculated analytically and numerically (FEM). The analytical model is
described based on bibliography, moreover, the numerical FEM model is developed with
the use of the SolidWorks software. The results i.e. the stresses obtained by analytical
and numerical calculation are compared and specified in Tables and Figures.
REFERENCES (14)
1.
Alexandrov A.V., Potapov V.D., Derzhavin B.P., Strength of materials, Moscow, Izd. ”Vyshaya Shkola” 2003. (in Russian).
2.
Attarnejad R., Semnani S.J., Shahba A., Analysis of non-prismatic Timoshenko beams using basic displacement functions, Advances in Structural Engineering, 14(2): 319-332, 2011.
3.
Auciello N.M., Ercolano A., A general solution for dynamic response of axially loaded non-uniform Timoshenko beams, International Journal of Solids and Structures, 41(18-19): 4861-4874, 2004.
4.
Auricchio F., Balduzzi G., Lovadina C., The dimensional reduction approach for 2D nonprismatic beam modelling: A solution based on Hellinger–Reissner principle, International Journal of Solids and Structures, 63: 264-276, 2015.
5.
Balduzzi G., Aminbaghai M., Sacco E., Füssl J., Eberhardsteiner J., Auricchio F., Non-prismatic beams: A simple and effective Timoshenko-like model, International Journal of Solids and Structures, 90: 236-250, 2016.
6.
Dado M., Al-Sadder S., A new technique for large deflection analysis of non-prismatic cantilever beams, Mechanics Research Communications, 32(6): 692-703, 2005.
7.
Gere J.M., Timoshenko S.P., Mechanics of Materials, (Second Edition) Boston, PWS-KENT Pub. Comp. 1984.
8.
Maalek S., Shear deflections of tapered Timoshenko beams, International Journal of Mechanical Sciences, 46(5): 783-805, 2004.
9.
Magnucki K., Lewinski J., Analytical modeling of Ibeam as a sandwich structures, Engineering Transactions, 66(4): 357-373, 2018.
10.
Rajasekaran S., Buckling of fully and partially embedded non-prismatic columns using differential quadrature and differential transformation methods, Structural Engineering and Mechanics, 28(2): 221-238, 2008.
11.
Rajasekaran S., Free vibration of centrifugally stiffened axially functionally graded tapered Timoshenko beams using differential transformation and quadrature methods, Applied Mathematical Modelling, 37(6): 4440-4463, 2013.
12.
Shahba A., Attarnejad R., Marvi M.T., Hajilar S., Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions, Composites Part B: Engineering, 42(4): 801-808, 2011.
13.
Slivker V.I., Structural mechanics, Moscow, Pub. Assoc. Structural 2005. (in Russian).
14.
Zhou D., Cheung K., Vibrations of Tapered Timoshenko Beams in Terms of Static Timoshenko Beam Functions, Journal of Applied Mechanics, 68(4): 596-602, 2001.
We process personal data collected when visiting the website. The function of obtaining information about users and their behavior is carried out by voluntarily entered information in forms and saving cookies in end devices. Data, including cookies, are used to provide services, improve the user experience and to analyze the traffic in accordance with the Privacy policy. Data are also collected and processed by Google Analytics tool (more).
You can change cookies settings in your browser. Restricted use of cookies in the browser configuration may affect some functionalities of the website.
You can change cookies settings in your browser. Restricted use of cookies in the browser configuration may affect some functionalities of the website.