PL EN
 
PL EN
Bieżący numer
Online first
Archiwum
O czasopiśmie
Informacja dla autorów
1/2010
Wyświetlenia: 14
CC-BY 4.0
Pobierz cytowanie
Optymalny projekt przemieszczania wagonów próżnych w hierarchicznych strukturach transportu kolejowego
Tadeusz Cisowski 1
 
 
 
Więcej
Ukryj
1
Wyższa Szkoła Ekonomii i Innowacji w Lublinie
 
 
Data publikacji: 02-02-2010
 
 
Rail Vehicles/Pojazdy Szynowe 2010,1,3-8
DOI: https://doi.org/10.53502/RAIL-139709
 
 
Artykuł (PDF)
Referencje (7)
 
STRESZCZENIE
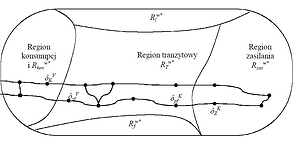
W pracy przedstawiono nowe, efektywne rozwiązanie zadania zarządzania parkiem wagonów próżnych. Opracowano model i algorytm optymalnego rozdziału wagonów próżnych, oparty na czterech ważnych zasadach: dekompozycji, agregacji informacji, koordynacji i dezagregacji. Zaproponowany model dekompozycyjny można efektywnie stosować zarówno do korekty planów okresowych, jak również do planowania bieżącego przemieszczania wagonów próżnych.
 
REFERENCJE (7)
1.
Hall A.D.: Podstawy teorii systemów. PWN, Warszawa 1968.
Google Scholar
 
 
2.
Тулупов Л.П., Митасов П.В, Пеккер А.Д.: Регулирование парка порожних вагонов с учетом их годности под огрузку. Вестник ВНИИЖТ, 1981, №3.
Google Scholar
 
 
3.
Niestierow E. P.: Programowanie liniowe w transporcie. WKiŁ, Warszawa 1974.
Google Scholar
 
 
4.
Кутыркин А.В., Кадушин А. И.: Полиопти-мизационная модель регулирования порожних вагонопотоков в АСУЖТ. Труды МИИТа, вып. 637,1979.
Google Scholar
 
 
5.
Лэсдон Л.С.: Оптимизация больших систем. «Наука», 1975.
Google Scholar
 
 
6.
Dantzig G.B.: Programming in linear structure. Econometrica 1949.
Google Scholar
 
 
7.
Месарович М., Мако Д., Такахара И.: Теория иерархических многоуровневых систем. М. «Мир», 1973.
Google Scholar
 
 
Udostępnij
Wyślij mailem
Indeksy
 
Indeks słów kluczowych
Indeks autorów
eISSN:2719-9630
ISSN:0138-0370
Journals System - logo
© 2006-2024 Journal hosting platform by Bentus
Scroll to top