PRACA ORYGINALNA
Free flexural vibrations of standard wide-flange H-beams with consideration of the shear effect
1
Łukasiewicz Research Network - Poznan Institute of Technology, 6 Ewarysta Estkowskiego St., 61-755 Poznań, Poland
Data nadesłania: 18-03-2024
Data ostatniej rewizji: 20-05-2024
Data akceptacji: 24-05-2024
Data publikacji online: 25-05-2024
Data publikacji: 16-11-2024
Autor do korespondencji
Krzysztof Magnucki
Łukasiewicz Research Network – Poznan Institute of Technology, Łukasiewicz Research Network – Poznan Institute of Technology, Polska
Łukasiewicz Research Network – Poznan Institute of Technology, Łukasiewicz Research Network – Poznan Institute of Technology, Polska
Rail Vehicles/Pojazdy Szynowe 2024,1-2,46-50
SŁOWA KLUCZOWE
Analytical studiesFundamental natural frequencyShear deformation theoryH-steel beamsZhuravsky shear stress
DZIEDZINY
STRESZCZENIE
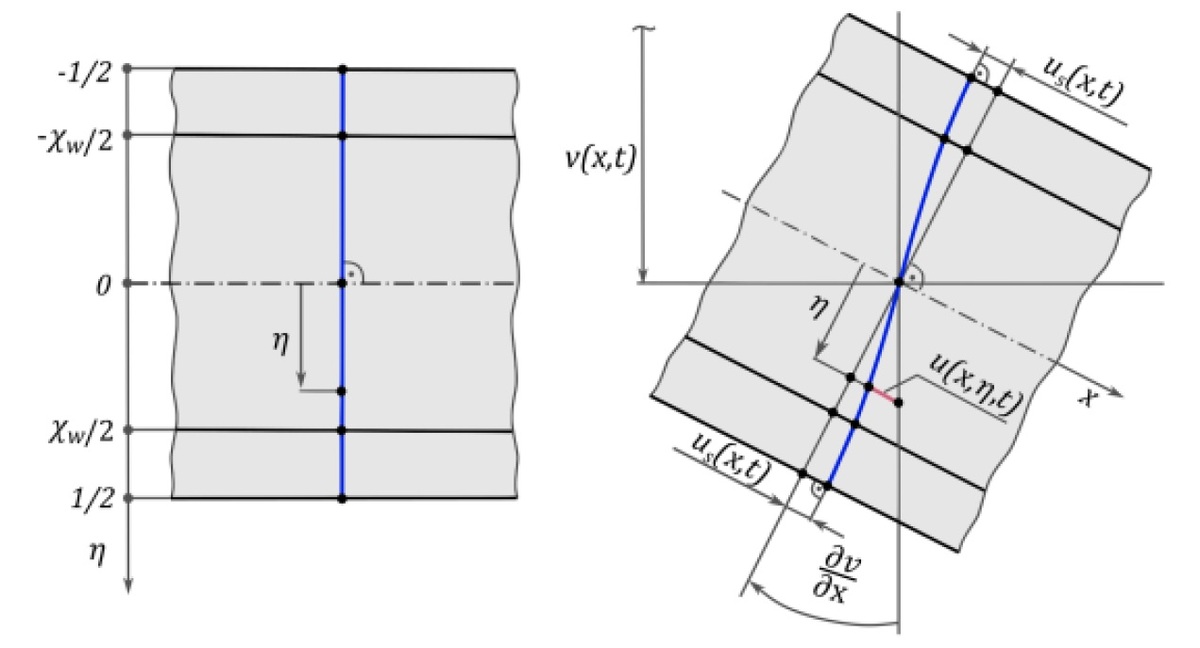
The subject of the paper is a simply supported standard wide-flange H-beam. Cross sections of this beam is analytically described as a three-layer structure. The shear effect in its succesive layers is taking into account with consideration of the classical shear stress formula called Zhuravsky shear stress. Based on Hamilton’s principle, two differential equations of motion are obtained. These equations are analytically solved and the fundamental natural frequency of flexural vibration for this beam is derived. Examplary calculations are carried out for selected five I-beams.
REFERENCJE (16)
1.
Aghababaei R, Reddy JN. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J Sound Vib. 2009;326:277-289. https://doi.org/10.1016/j.jsv.....
2.
Akgöz B, Civalek Ö. A size-dependent shear deformation beam model based on the strain gradient elasticity theory. Int J Eng Sci. 2013;70;1-14. https://doi.org/10.1016/j.ijen....
3.
Ghugal YM, Sharma R. A hyperbolic shear deformation theory for flexure and vibration of thick isotropic beams. Int J Comput Methods. 2009;6(4):585-604. https://doi.org/10.1142/S02198....
4.
Guo Q, Shi G. An accurate and efficient 4-noded quadrilateral plate element for free vibration analysis of laminated composite plates using a refined third-order shear deformation plate theory. Compos Struct. 2023;324:117490. https://doi.org/10.1016/j.comp....
5.
Magnucki K. Bending of symmetrically sandwich beams and I-beams – analytical study. Int J Mech Sci. 2019;150:411-419. https://doi.org/10.1016/j.ijme....
6.
Magnucki K, Lewinski J, Magnucka-Blandzi E. A shear deformation theory of beams with bisymmetrical cross-section based on the Zhuravsky shear stress formula. Engineering Transactions. 2020;68(4):353-370. https://doi.org/10.24423/EngTr....
7.
Magnucki K. An individual shear deformation theory of beams with consideration of the Zhuravsky shear stress formula. In: Zingoni A (ed.) Current perspectives and new directions in mechanics, modelling and design of structural systems. CRC Press, Taylor & Francis Group. London, New York 2022:682-689. https://doi.org/10.1201/978100....
8.
Mahi A, Bedia EAA, Tounsi A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl Math Model. 2015;39:2489-2508. https://doi.org/10.1016/j.apm.....
9.
Nguyen T-K, Nguyen TT-P, Vo TP, Thai H-T. Vibration and buckling analysis of functionally graded sandwich beams by a new higher-order shear deformation theory. Compos Part B-Eng. 2015;76:273-285. https://doi.org/10.1016/j.comp....
10.
Reddy JN. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci. 2010;48:1507-1518. https://doi.org/10.1016/j.ijen...
11.
Ren S, Cheng C, Meng Z, Yu B, Zhao G. A new general third-order zigzag model for asymmetric and symmetric laminated composite beams. Compos Struct. 2021;260:113523. https://doi.org/10.1016/j.comp....
12.
Sawant M, Dahake AG. A new hyperbolic shear deformation theory for analysis of thick beam. International Journal of Innovative Research in Science, Engineering and Technology. 2014;3(2):9636-9643. https://www.researchgate.net/p....
13.
Sobhy M. An accurate shear deformation theory for vibration and buckling of FGM sandwich plates in hygrothermal environment. Int J Mech Sci. 2016;110:62-77. http://doi.org/10.1016/j.ijmec....
14.
Thai H-T, Vo TP. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int J Mech Sci. 2012;62:57-66. https://doi.org/10.1016/j.ijme....
15.
Thai S, Thai H-T, Vo TP, Patel VI. A simple shear deformation theory for nonlocal beams. Compos Struct. 2018;183:262-270. https://doi.org/10.1016/j.comp....
16.
Xiang S. A new shear deformation theory for free vibration of functionally graded beams. Appl Mech Mater. 2014;455:198-201. https://doi.org/10.4028/www.sc....
CYTOWANIA (1):
1.
A shear effect in a bending non-standard I-beam under uniformly distributed load
Ewa Magdalena Magnucka-Blandzi, Krzysztof Magnucki
Rail Vehicles/Pojazdy Szynowe
Ewa Magdalena Magnucka-Blandzi, Krzysztof Magnucki
Rail Vehicles/Pojazdy Szynowe
Przetwarzamy dane osobowe zbierane podczas odwiedzania serwisu. Realizacja funkcji pozyskiwania informacji o użytkownikach i ich zachowaniu odbywa się poprzez dobrowolnie wprowadzone w formularzach informacje oraz zapisywanie w urządzeniach końcowych plików cookies (tzw. ciasteczka). Dane, w tym pliki cookies, wykorzystywane są w celu realizacji usług, zapewnienia wygodnego korzystania ze strony oraz w celu monitorowania ruchu zgodnie z Polityką prywatności. Dane są także zbierane i przetwarzane przez narzędzie Google Analytics (więcej).
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.