RESEARCH PAPER
A shear effect in a bending non-standard I-beam under uniformly distributed load
1
Institute of Mathematics, Poznan University of Technology, Polska
2
Łukasiewicz Research Network - Poznan Institute of Technology, 6 Ewarysta Estkowskiego St., 61-755 Poznań, Poland
These authors had equal contribution to this work
Submission date: 2024-10-02
Final revision date: 2025-01-12
Acceptance date: 2025-01-15
Online publication date: 2025-01-19
Publication date: 2025-02-27
Corresponding author
Ewa Magdalena Magnucka-Blandzi
Institute of Mathematics, Poznan University of Technology, Piotrowo, 60-965, Poznan, Polska
Institute of Mathematics, Poznan University of Technology, Piotrowo, 60-965, Poznan, Polska
Rail Vehicles/Pojazdy Szynowe 2024,3-4,28-35
KEYWORDS
TOPICS
ABSTRACT
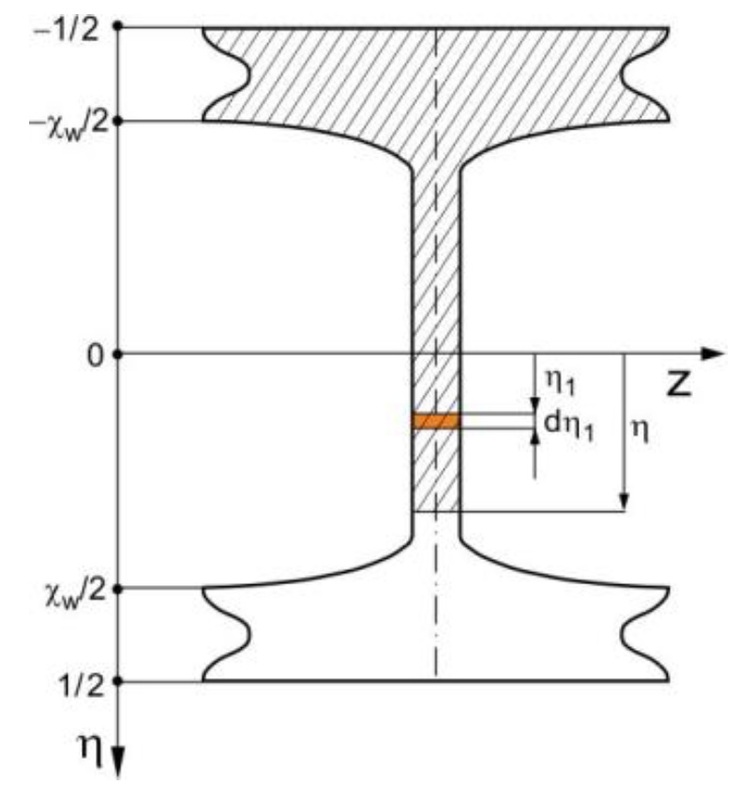
The paper is devoted to the analytical study of the bending problem of a simply supported or clamped non-standard I-beam under a uniformly distributed load. The cross-sectional shape of this beam, as a three-part structure, is analytically described. The purpose of this research is to present a detailed analytical model of this beam, considering the shear effect and its influence on the beam's deflection. This model is formulated according to linear elastic theory, and the deformation of a planar cross-section after the bending of this beam due to the shear effect is determined. Based on the principle of stationary potential energy, two differential equations of equilibrium are obtained. These equations are analytically solved, and the dimensionless shear effect function and the relative deflection of this beam are derived. Consequently, the maximum dimensionless relative deflection and the dimensionless coefficient of the shear effect are determined. Exemplary calculations are carried out for three selected non-standard I-beams of different lengths, demonstrating a significant influence of the shear effect on the deflections of short beams, especially clamped beams.
REFERENCES (21)
1.
Akgöz B, Civalek Ö. A size-dependent shear deformation beam model based on the strain gradient elasticity theory. Int J Eng Sci. 2013;70:1-14. https://doi.org/10.1016/j.ijen....
2.
Bardella L, Mattei O. On explicit analytic solutions for the accurate evaluation of the shear stress in sandwich beams with a clamped end. Compos Struct. 2014;112:157-168. https://doi.org/10.1016/j.comp....
3.
Elishakoff I, Kaplunov J, Nolde E. Celebrating the centenary of Thimoshenko’s study of effects of shear deformation and rotary inertia. Appl Mech Rev. 2015;67:060802. https://doi.org/10.1115/1.4031....
4.
Genovese D, Elishakoff I. Shear deformable rod theories and fundamental principles of mechanics. Arch Appl Mech. 2019;89:1995-2003. https://doi.org/10.1007/s00419....
5.
Ghugal YM, Sharma R. A hyperbolic shear deformation theory for flexure and vibration of thick isotropic beams. Int J Comput Methods. 2009;6(4):585-604. https://doi.org/10.1142/S02198....
6.
Kustosz J, Magnucki K, Goliwąs D. Strength of a bent sandwich beam with clamped ends. Rail Vehicles/Pojazdy Szynowe. 2023;1-2:3-7. https://doi.org/10.53502/RAIL-....
7.
Magnucki K. Bending of symmetrically sandwich beams and I-beams – analytical study. Int J Mech Sci. 2019;150:411-419. https://doi.org/10.1016/j.ijme....
8.
Magnucki K, Lewinski J, Magnucka-Blandzi E. A shear deformation theory of beams with bisymmetrical cross-section based on the Zhuravsky shear stress formula. Engineering Transactions. 2020;68(4):353-370. https://doi.org/10.24423/EngTr....
9.
Magnucki K, Witkowski D. Effective shaping of a bisymmetrical cross section of beams under shear stresses constraints. IOP Conf Ser: Mater Sci Eng. 2021;1199:012062. https://doi.org/10.1088/1757-8....
10.
Magnucki K. An individual shear deformation theory of beams with consideration of the Zhuravsky shear stress formula. In: Zingoni A (ed.). Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems, CRC Press, Taylor & Francis Group, Boca Raton, London, New York 2022;682-689. https://doi.org/10.1201/978100....
11.
Magnucki K, Magnucka-Blandzi E. A refined shear deformation theory of an asymmetric sandwich beam with porous core: linear bending problem. Appl Math Model. 2023;124:624-638. https://doi.org/10.1016/j.apm.....
12.
Magnucki K, Sowiński K. Bending of a sandwich beam with an individual functionally graded core. J Theor App Mech. 2024;62(1):3-17. https://doi.org/10.15632/jtam-....
13.
Magnucki K, Magnucka-Blandzi E, Witkowski D, Stefańska N. Bending of a homogeneous beam with a monosymmetric cross section – shear effect. Engineering Transactions. 2024;72(3):285-307. https://doi.org/10.24423/EngTr....
14.
Magnucki K. Free flexural vibrations of standard wide-flange H-beams with consideration of the shear effect. Rail Vehicles/Pojazdy Szynowe. 2024;1-2:46-50. https://doi.org/10.53502/RAIL-....
15.
Mahi A, Bedia EAA, Tounsi A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl Math Model. 2015;39:2489-2508. https://doi.org/10.1016/j.apm.....
16.
Reddy JN. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci. 2010;48:1507-1518. https://doi.org/10.1016/j.ijen....
17.
Ren S, Cheng C, Meng Z, Yu B, Zhao G. A new general third-order zigzag model for asymmetric and symmetric laminated composite beams. Compos Struct. 2021;260:113523. https://doi.org/10.1016/j.comp....
18.
Sawant M, Dahake AG. A new hyperbolic shear deformation theory for analysis of thick beam. International Journal of Innovative Research in Science, Engineering and Technology. 2014;3(2):9636-9643. https://www.researchgate.net/p....
19.
Thai S, Thai H-T, Vo TP, Patel VI. A simple shear deformation theory for nonlocal beams. Compos Struct. 2018;183:262-270. https://doi.org/10.1016/j.comp....
20.
Wang CM, Reddy JN, Lee KH. Shear deformable beams and plates. Relationships with classical solutions. Elsevier: Amsterdam, Lausanne, New York, Oxford, Shannon, Singapore, Tokyo 2000.
21.
Ziemian CW, Ziemian RD. Numerical investigation of the influence of transverse welds on the strength of aluminum alloy I-shape members – beams. Structures. 2024;60:105861. https://doi.org/10.1016/j.istr....
We process personal data collected when visiting the website. The function of obtaining information about users and their behavior is carried out by voluntarily entered information in forms and saving cookies in end devices. Data, including cookies, are used to provide services, improve the user experience and to analyze the traffic in accordance with the Privacy policy. Data are also collected and processed by Google Analytics tool (more).
You can change cookies settings in your browser. Restricted use of cookies in the browser configuration may affect some functionalities of the website.
You can change cookies settings in your browser. Restricted use of cookies in the browser configuration may affect some functionalities of the website.